题解 P2444 【[POI2000]病毒】

发表于 | 更新于

题意:给定$n$个$01$串，保证$01$串长度之和不超过$30000$，询问是否存在无限长的$01$串，使得给定串都不是它的子串。

很考验对$fail$指针的理解,假设我们构造出了一个无限长的安全代码，再到$AC$自动机上匹配，从原点出发，向下走遇到一个环，然后不停地在这个环上跳转(无法理解就手玩样例)，且这个环上没有危险节点(即病毒单词最后一个字母在$Trie$树上的位置)

注意：这个环不包括$fail$指针,但是包括优化边(即如果节点$i$的某个字符儿子为空，那么这个儿子存为$i$的$fail$指针指向的节点的相同字符儿子)(有点绕,放张样例构成的$trie$图)

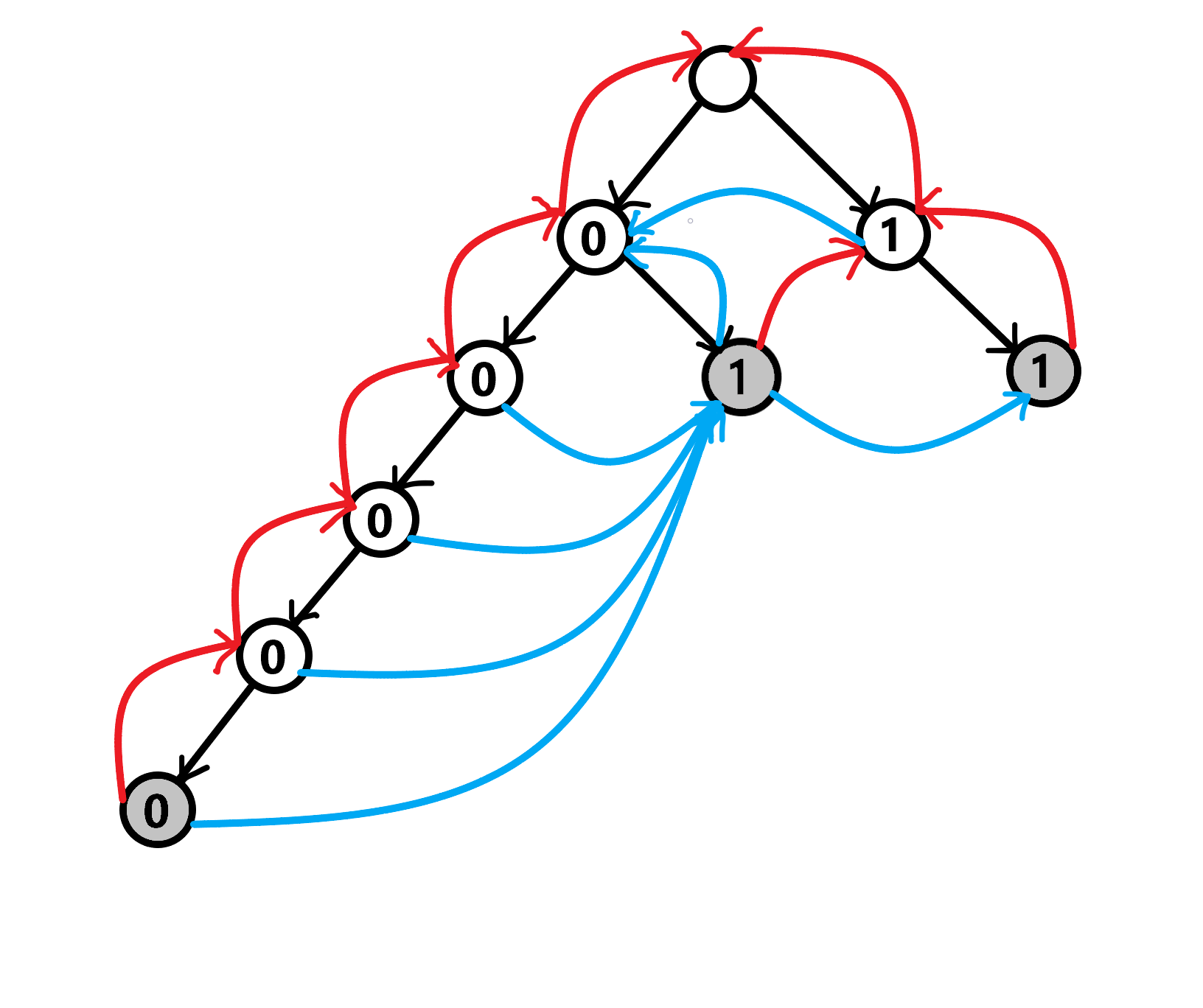
黑边是$trie$树上的正常边，蓝边是在处理$AC$自动机时连上的优化边，红边是$fail$指针。灰色节点即危险节点

这里的环只由蓝边和黑边构成的，即不考虑走$fail$指针，

这样，问题就变成了找一个从根节点出发能在不经过危险节点的情况下走到到的环，且环上没有危险节点。

注意：如果某个点的$fail$指针指向的点是有危险节点，那么该节点也是危险节点

接下来$dfs$找环，找到就输出属于基础图论。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
#define ll long long
#define re register
#define inf 0x3f3f3f3f
#define N 1000007
using namespace std;
struct node{
    int fail,cnt,ch[2];
}f[N>>1];
inline int read(){
    int x=0,w=0;char ch=getchar();
    while (!isdigit(ch))w|=ch=='-',ch=getchar();
    while (isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
    return w?-x:x;
}
int ans,cnt,ok[N],vis[N];
char s[N];
queue<int>q;
inline void build(char *s){
    int len=strlen(s),now=0;
    for (int i=0;i<len;++i){
        int v=s[i]-'0';
        if (!f[now].ch[v])f[now].ch[v]=++cnt;
        now=f[now].ch[v];
    }
    f[now].cnt=1;
}
inline void build_fail(){
    for (int i=0;i<2;++i)if (f[0].ch[i])q.push(f[0].ch[i]);
    while (!q.empty()){
        int u=q.front();q.pop();
        for (int i=0;i<2;++i)
            if (f[u].ch[i]){
                f[f[u].ch[i]].fail=f[f[u].fail].ch[i];
                f[f[u].ch[i]].cnt|=f[f[f[u].fail].ch[i]].cnt;
                q.push(f[u].ch[i]);
            }else f[u].ch[i]=f[f[u].fail].ch[i];
    }
}
void dfs(int now){
    if (ok[now]){puts("TAK");exit(0);}
    if (vis[now]||f[now].cnt)return;
    vis[now]=ok[now]=1;
    if (f[now].ch[0])dfs(f[now].ch[0]);
    if (f[now].ch[1])dfs(f[now].ch[1]);
    ok[now]=0;
}
signed main(){
    int n=read();
    for (int i=1;i<=n;++i){
        scanf("%s",s);
        build(s);
    }
    build_fail();
    dfs(0);
    puts("NIE");
    return 0;
}